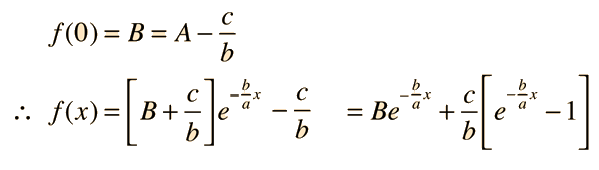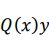ENSAYO TRIAXIAL

El esfuerzo cortante en los suelos es el aspecto más importante de la ingeniería geotécnica. La capacidad de soporte de cimentaciones superficiales como profundas, la estabilidad de los taludes y el diseño de muros o paredes de retención, llevan implícito el valor de la resistencia al esfuerzo cortante. Desde otro punto de vista, el diseño de los pavimentos, se ve influenciado de una forma indirecta por la resistencia al cortante de los suelos, ya sea en el análisis de la estabilidad de un talud o en el diseño de los muros de retención y de forma directa, a través del diseño de las fundaciones que soportan el pavimento, específicamente, en la subrasante. Por consecuencia, tanto las estructuras como los taludes deben ser estables y seguros frente a un colapso total, cuando éstos sean sometidos a una máxima aplicación de cargas.

Ecuacion Diferencial de Riccati

DEFINICION:

La ecuación de Riccati es una ecuación diferencial ordinaria, no lineal de primer orden, inventada y desarrollada en el siglo XVIII por el matemático italiano Jacopo Francesco Riccati, con el fin de analizar la hidrodinámica.En 1724 publicó una investigación multilateral de la ecuación, llamada, por iniciativa de D'Alembert (1769): Ecuación de Riccati. La investigación de la ecuación de Riccati convocó el esfuerzo de varios matemáticos: Leibniz, Goldbach, Juan Bernoulli y sus hijos Nicolás y Daniel Bernoulli, y posteriormente, a Euler.1

Generalmente, esta ecuación la presentan en la forma:

EJERCICIO N.1:

Recibe el nombre de ecuación de Riccati toda ecuación diferencial de la forma:

En general, esta ecuación no se integra en cuadraturas (la búsqueda de la solución no puede reducirse a un

número finito de integraciones sucesivas).

Si se conoce una solución particular, y1(x), entonces, introduciendo una nueva variable z tal que:

La ecuación diferencial de Riccati se reduce a una ecuación diferencial lineal puesto que podemos poner:

Y sustituyendo en (R1):

Pero teniendo en cuenta que y1 es solución de (R1) se verificará:

Por lo que sustituyendo y simplificando tendremos:

Que es una ecuación lineal en z.

Integrada esta última ecuación y hallada z, se podrá pasar a y por la equivalencia dada.

Si se conoce otra solución más, y2, de la ecuación diferencial del Riccati, entonces:

Es una solución particular de la ecuación lineal para la variable z, lo cual nos permite simplificar su integración.

Si para la ecuación diferencial de Riccati se conocen tres soluciones particulares y1, y2 e y3, entonces su integral

general es:

Resultado que se puede enunciar diciendo que la razón doble de cuatro integrales particulares de la ecuación

diferencial de Riccati es constante.

EJERCICIO N.2:

Es una ecuación de Riccati. Veamos que efectivamente Y1=x es solución de la ecuación

Efectuando la sustitucion Y= x + 1/ v

Simplificando, queda la ecuacion lineal  v´+  v = x, cuya solucion general es

Veamos el siguiente video, para mejor compresión:

Ecuacion Diferencial de Bernoulli

DEFINICION:

En dinámica de fluidos, el principio de Bernoulli, también denominado ecuación de Bernoulli o trinomio de Bernoulli, describe el comportamiento de un líquido moviéndose a lo largo de una corriente de agua. Fue expuesto por Daniel Bernoulli en su obra Hidrodinámica (1738) y expresa que en un fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación por un conducto cerrado, la energía que posee el fluido permanece constante a lo largo de su recorrido.

Ejercicio N.1:

Una ecuación diferencial que tenga en la forma

Se denomina una ecuación diferencial de Bernoulli. Dicha ecuación no es lineal, ya el segundo término de la igualdad viene en función de la variable dependiente y para encontrar la solución general, es conveniente considera una ecuación equivalente que sea lineal, para ello multiplicamos la ecuación dada por y^(-n) ,quedando la ecuación en la forma

Ahora, si se realiza el siguiente cambio de variable U=y ^1-n su derivada seria

 De donde, la ecuación se transforma en

La cual se puede escribir como

EJERCICIO N.2:

Paso1: usamos la ecuación de y=u^1-n

Paso 2 : sustitimos 

Paso 3: dividimos todo en -x^2 u^-2

Paso 4: encontrar el factor integrante con la siguiente formula

Paso 5: multiplicamos toda f(x) por el factor integrante

Paso 6: cancelamos la integral con la derivada y al otro lado integramos

Paso 7: ponemos todo en términos de (x)y (y)

Paso 8:

Para complemetar la explicacion dejaremos el siguiente video:

Ecuacion diferencial lineal no Homogénea

INFORMACION:

Los sistemas de ecuaciones diferenciales lineales no homogéneos son de la forma

  x´ = A(t)x + b(t)

donde, para cada t, A(t) es una matriz n×n, x es un vector columna de funciones incógnita y b(t) es un vector columna de funciones conocidas. 

La forma de proceder para resolver este tipo de sistemas es la misma que ya estudiamos para las ecuaciones diferenciales lineales no homogéneas . Primero demostraremos que la solución general del sistema es la suma de la solución general del sistema homogéneo 

x´= A(t)x 

y de una solución particular del no homogéneo. A continuación diseñaremos un método para encontrar una solución particular del sistema no homogéneo. 

Ejercicio N.1

RESOLUCIÓN DE UNA ECUACIÓN DIFERENCIAL LINEAL NO HOMOGÉNEA DE PRIMER ORDEN:

Ejercicio N:2

Donde a,b,c son constantes.

Para resolver una ecuación diferencial lineal no homogénea es importante tener en cuenta los siguientes pasos:

Iniciamos verificando que la ecuación es NO homogénea.

Si tenemos que C=0  podemos decir que a ecuación no es homogénea y añade un paso mas en el proceso de solución de la misma. El camino hacia una solucion general pasa por encontrar previamente una solución a la ecuacion homogénea (es decir, quitar la constante c), y luego encontrar una solución particular a la ecuación no homogénea (es decir, encontrar cualquier solución considerando la constante c como parte de la ecuación). La solución a la ecuación homogénea es

Por sustitución, se puede verificar que estableciando esta función igual al valor constante -c/b satisfacerá a la ecuación no homogénea.

Forma parte de la naturaleza de las ecuaciones diferenciales, que la suma de soluciones sea también otra solución, de modo que tomando la suma de las dos soluciones de arriba, se puede aproximar a una solución general. El requisito final para la aplicación de la solución al problema físico es que la solución encuentre las condiciones de contorno físicas del problema. La situación mas normal en los problemas físicos, es que las condiciones de contorno (condiciones de frontera) son los valores de la función f(x) y sus derivadas cuando x=0. Las condiciones de contorno a menudo se llaman "condiciones iniciales". Para la ecuación de primer orden, necesitamos especificar una condición de contorno. Por ejemplo:

Sustituyendo para x=0 da:

Tambien podemos ver el siguiente video: